今年（2024年）的明日方舟国服愚人节活动是一个赛博斗蛐蛐活动。活动的玩法是这样的：

  1. 用一套权重流程，从26个兵种中不重复地选出一些种类，数量各异的怪
  2. 生成一个场地地图
  3. 把怪按种类大致均分到两侧，然后让他们大致随机地从两侧的门刷出。
  4. 两侧怪物大致刷出一半到全部时暂停游戏，玩家选边押注。
  5. 怪物继续自然行进，互相攻击。
  6. 双方互相攻击直到一方全部死亡，此时另一方获胜。同时死亡则均判定为获胜。

这是一个比较经典的活动链接。【我是链接】活动本身很有意思，近战、远程怪有很复杂的循环克制关系，部分刷得很多的怪，比如虫子和狗子，对其刷出的数量非常敏感，更不用提实战中各种逆天走位、卡位和令人窝火的转火。活动本身在社区引起了极大的讨论度，玩家切切实实体会到了当赛博王爷的乐趣。

兴奋之余我在想，是否能够通过机器学习（深度学习）的手段，在选边押注阶段，就能预测出一局斗蛐蛐的结果？

问题分析和建模

机器学习解决实际问题，首先需要明确问题的各种变量，以及这些变量中哪些是能提取的。

首先最容易统计的数据就是两侧的怪物的种类和各自数量，以及地图的障碍物情况。这些也是游戏直接显示给玩家的。

其他变量包括但不限于刷怪数量的产生过程、怪从出生点刷出时的分布和先后，怪的走位和索敌等等。

该问题中，刷怪的权重机制已经有详细的解析【我是链接】，总结一下就是：

单局有权重 $W$，第k种怪的第n只消耗权重 $w(k,n)=w_{k,0}+\Delta w_k$；
单局内的各种怪按照一定顺序消耗权重，直到权重耗尽或无法再刷出选定的任意一种怪为止。

但是每局的权重有轻微的浮动，这导致我们不能将其作为一个比较好的变量。

统计的一千多条数据中，只有极少数地图有障碍物，但是对战局的影响非常大（比如让远程怪从集火射击变成排队送人头），因此决定保留为变量之一。

另外，刷怪规律、索敌机制、转火机制等在实战中也有很大的影响【咸鱼错题集】，但是出于方便，这里不将它们作为变量。

因此，本问题建模如下：

使用一个26+1=27维度的向量记录押注界面的情况。前26个维度记录各个兵种对应的怪物数量，第27个特征记录地图情况。

对于左侧的怪物，兵力按照显示的记录；对于右侧的怪物，兵力按照显示的兵力数乘以>1，其他未出现的兵种记0.

比如左侧40条狗对右侧1个石头人，则狗一栏记40，石头人记>1，其他未出现的怪物记0.

若左侧胜，结果记录为0；右侧胜，结果记录为1.

这样我们得到了一个27+1=28列的数据集，问题本身也抽象成了一个二元分类问题。

数据收集

本次共收集到1756条对局数据。

数据来源 数据数量
B站@Encientea 1120
NGA@喜欢做作业的alien[注] 65
Discord热心群友 65
QQ群友帕鲁们 520
合计 1756

[注]

  1. 帖主自己记录了200条数据，我手动转录了前51条（太难受了眼睛疼）
  2. 下面有人跟帖又补了一些数据，不过格式比较抽象，暂时不做录入。

我和一些B站网友交流后觉得可以使用cv直接识别视频和图片以代替人工，奈何参与讨论的网友们没一个人懂cv，只能作罢。

数据都有了那么直接开干吧！
整个项目我上传到了 github【链接】

数据初步分析，主成分分析

首先容易看出，两侧的胜率基本是一致的（ 左侧胜：右侧胜 = 832 : 805 = 50.82% : 49.18%）。这说明算法随机性足够，我们有理由相信两侧胜率都是50%【提一下卡方检验的值是多少】；同时这也为机器学习的预测准确率划下了大致50%的底线——算法结果总不能不如盲选吧！

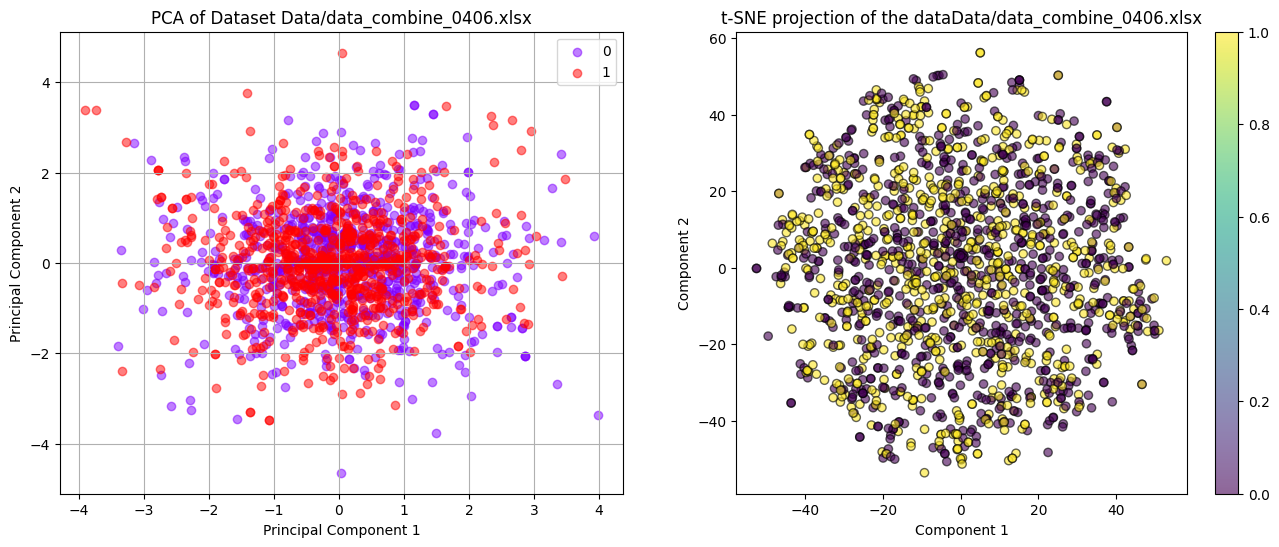
使用PCA方法和t-SNE方法，将数据降到二维，进行可视化分析。

1
2
3
4
5
6
7
8
9
10
#先看看你的成分
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, classification_report
from sklearn.preprocessing import StandardScaler

file_paths=['Data/data_combine_0406.xlsx']
#file_paths=['Data/data_0405.xlsx','Data/data_combine_0405.xlsx']

图1：PCA方法和t-SNE方法结果

可以看到，所有数据全部糊在一起，你中有我我中有你，这意味着：

  1. 数据线性不可分，基于线性模型的机器学习方法无法很好区别0和1；
  2. 数据可能在高维度有复杂结构，这些结构在降低维度后无法清晰展现；
  3. 可能存在噪声和异常值，需要清洗和预处理；但是上面的所有数据都是人肉统计的，基本不会有问题，本条排除；
  4. 本问题使用线性机器学习算法解决不了，需要非线性的核函数或者类似神经网络等算法参与分析。

机器学习算法的过滤法，嵌入法，包装法

本段使用ChatGPT帮助总结

在二元分类问题中，特征选择是一个重要步骤，它涉及选择对于预测目标变量最有帮助的特征集合。这不仅可以提高模型的性能，还可以减少计算成本并提高模型的可解释性。特征选择方法通常分为三种类型：过滤法（Filter methods）、包装法（Wrapper methods）和嵌入法（Embedded methods）。

过滤法

过滤法基于统计测试评价、排序各个特征，并选择得分最高的特征。

  • 简单好用
  • 在选择模型前就能完成特征选择。
  • 适用于早期检验和特征维数非常高的时候
  • 不需要建立模型（其实就是纯统计方法）
  • 速度快，计算效率高
  • 忽略了特征之间的相互作用

嵌入法

嵌入法将特征选择过程和模型训练过程结合起来。

  • 是最常见的特征选择方法
  • 在模型的训练过程中直接进行特征选择，边训练边摸索特征和目标变量的相互作用。
  • 更关注模型性能
  • 速度依赖各种模型本身

包装法

包装法根据目标预测模型的性能评估特征子集的好坏。

  • 依赖于目标预测模型的选取，一切在完成首轮嵌入法的训练后才开始
  • 计算成本很高，特征子集变化就要重头训练
  • 数据特征较少的时候，可能会过拟合

使用过滤法算法进行机器学习

其实可以直接调用scikit包的，回头看jyb的聊天记录补全这部分

说是机器学习，其实是用一些统计方法检验各个特征，比如卡方检验，相关系数排名等。

使用卡方检验，检验各变量各自和结果的关系

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#卡方检验
import pandas as pd
from scipy.stats import chi2_contingency

# 初始化一个空的字典来保存每个特征的卡方检验结果
chi2_results = {}

# 对file_paths列表中的每个文件路径进行遍历
for file_path in file_paths:
    # 读取数据文件
    df = pd.read_excel(file_path)

    # 遍历所有的特征列，除了最后一列，因为最后一列是目标变量
    for feature in df.columns[:-1]:
        # 构建列联表，每个特征与结果的列联表
        crosstab = pd.crosstab(df[feature], df['结果'])
        # 执行卡方检验
        chi2, p, dof, expected = chi2_contingency(crosstab)
        # 将结果保存到字典中
        chi2_results[feature] = {'Chi2': chi2, 'p-value': p, 'DOF': dof}

# 将卡方检验结果转换成DataFrame
chi2_df = pd.DataFrame(chi2_results).T  # 转置，让特征成为行索引

# 添加是否接受原假设列
chi2_df['是否接受原假设'] = ['拒绝' if p_value > 0.05 else '接受' for p_value in chi2_df['p-value']]
chi2_df_sorted = chi2_df.sort_values(by='p-value', ascending=False)
chi2_df_sorted

结果如下：

名称 Chi2 p-value DOF 是否接受原假设
窃笑鳄鱼 16.993774 9.312759e-01 27.0 拒绝
迟钝的持盾者 23.366898 6.651535e-01 27.0 拒绝
扎人的石头 12.378891 6.501530e-01 15.0 拒绝
地形 1.033476 5.964631e-01 2.0 拒绝
劈柴骑士 12.746314 4.675926e-01 13.0 拒绝
普通的萨卡兹 29.339031 3.954862e-01 28.0 拒绝
扩音术士 11.608379 3.121206e-01 10.0 拒绝
责罚者 11.736195 3.030999e-01 10.0 拒绝
衣架射手 34.319002 1.905669e-01 28.0 拒绝
冰手术士 29.560922 1.624255e-01 23.0 拒绝
流鼻涕虫虫 49.284545 1.251712e-01 39.0 拒绝
“庞贝” 13.485217 9.620966e-02 8.0 拒绝
弧光武士 24.667377 7.590788e-02 16.0 拒绝
狗pro 102.831665 6.915172e-02 83.0 拒绝
保鲜膜骑士 45.770133 6.874858e-02 33.0 拒绝
迫击炮投弹手 19.579389 5.145374e-02 11.0 拒绝
镜子机关枪 24.481147 4.004875e-02 14.0 接受
“火苗与软钢” 33.654900 3.944115e-02 21.0 接受
拳击宗师 44.841876 3.048136e-02 29.0 接受
锁链拳手 49.042711 2.750579e-02 32.0 接受
源石的腿脚 39.807610 1.138487e-02 22.0 接受
巧克力流星虫虫 68.148374 2.646780e-03 39.0 接受
奔跑吧!躯壳! 77.447075 1.104612e-04 37.0 接受
杰斯顿·威廉姆斯 28.933082 8.065927e-06 4.0 接受
苦难的具象 54.023628 5.139625e-06 16.0 接受
小寄居蟹 62.668315 7.527878e-07 18.0 接受
砸人的石头 48.722232 2.571740e-08 7.0 接受

由上可知拒绝“本兵种对结果没有影响”这个假设，即“本兵种对结果有影响”的兵种共计16个兵种，为上面从“窃笑鳄鱼”到“迫击炮投弹手”这一部分。

使用嵌入法算法进行机器学习

初步计算的代码和结果

这里使用以下机器学习算法进行计算：

  1. Logistic Regression
  2. 线性SVC
  3. SVM
  4. MLP
  5. GBM (Gradient Boosting Classifier)
  6. 随机森林
  7. 决策树

首先配置环境与模型参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#模型与参数
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
from sklearn.svm import SVC
from sklearn.neural_network import MLPClassifier
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.ensemble import RandomForestClassifier
from sklearn.tree import DecisionTreeClassifier

# 使用通用的函数处理多个文件和模型
models ={
            'Logistic Regression':LogisticRegression(max_iter=100000,random_state=42),
            'Linear SVC':LinearSVC(max_iter=1000000,random_state=42),
            'SVM with RBF kernel':SVC(kernel='rbf',max_iter=100000,random_state=42),
            'MLP classifier':MLPClassifier(hidden_layer_sizes=(100,), max_iter=10000, activation='relu', solver='adam', learning_rate_init=0.01,random_state=42),
            'Gradient Boosting Machine': GradientBoostingClassifier(n_estimators=100, learning_rate=0.1, max_depth=3, random_state=42),
            'Random Forest': RandomForestClassifier(n_estimators=100, random_state=42),
            'Decision Tree': DecisionTreeClassifier(random_state=42)
        }

使用各个算法时，分为是否使用 k-fold (k=10)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
#数据预处理和输出，分使用K-Fold和不使用K-Fold两种情况
from sklearn.model_selection import KFold, cross_val_score
def preprocess_data(file_path):
    #加载数据并进行预处理，返回分割后的训练集和测试集
    df = pd.read_excel(file_path, engine='openpyxl')
    X = df.iloc[:, :-1].values  # 特征
    y = df.iloc[:, -1].values   # 标签
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)
    X_train, X_test, y_train, y_test = train_test_split(X_scaled, y, test_size=0.2, random_state=42)
    return X_train, X_test, y_train, y_test

def train_evaluate_model(X_train, X_test, y_train, y_test, model):
    #训练模型并评估模型性能
    model.fit(X_train, y_train)
    y_pred = model.predict(X_test)
    accuracy = accuracy_score(y_test, y_pred)
    report = classification_report(y_test, y_pred)
    return accuracy, report

def preprocess_data_k_fold(file_path):
    #不使用k-fold加载数据并进行预处理
    df = pd.read_excel(file_path, engine='openpyxl')
    X = df.iloc[:, :-1].values  # 特征
    y = df.iloc[:, -1].values   # 标签
    scaler = StandardScaler()
    X_scaled = scaler.fit_transform(X)
    return X_scaled, y

def train_evaluate_model_k_fold(X, y, model, n_splits=10):
    #使用K折交叉验证来训练和评估模型
    kf = KFold(n_splits=n_splits, shuffle=True, random_state=42)
    scores = cross_val_score(model, X, y, cv=kf, scoring='accuracy')
    
    # 计算平均准确率
    average_accuracy = np.mean(scores)  
    return average_accuracy, scores

#输出结果，不用k_fold
def evaluate_models_on_datasets(file_paths, models):
    print('---------------------------------')
    for file_path in file_paths:
        X_train, X_test, y_train, y_test = preprocess_data(file_path)
        print('On dataset:', file_path)
        print('---------------------------------')
        for model_name, model in models.items():
            accuracy, report = train_evaluate_model(X_train, X_test, y_train, y_test, model)
            print(f'{model_name}'+'\'s accuracy:', accuracy)
            #print('Classification Report:', report)
        print('---------------------------------')

#输出结果，使用k_fold
def evaluate_models_on_datasets_k_fold(file_paths, models):
    print('---------------------------------')
    for file_path in file_paths:
        X, y = preprocess_data_k_fold(file_path)  # 修改为返回整个数据集
        print('On dataset:', file_path)
        print('---------------------------------')
        for model_name, model in models.items():
            # 修改为使用K折交叉验证
            accuracy, scores = train_evaluate_model_k_fold(X, y, model)
            print(f'{model_name}'+'\'s accuracy:', accuracy)
            #print('Accuracy for each fold:', scores)
        print('---------------------------------')

对数据使用算法吧！

1
2
3
4
#不使用k-fold交叉验证
evaluate_models_on_datasets(file_paths, models)
#使用k-fold交叉验证
evaluate_models_on_datasets_k_fold(file_paths, models)

结果如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 不使用k-fold
---------------------------------
On dataset: Data/data_combine_0406.xlsx
---------------------------------
Logistic Regression's accuracy: 0.6951219512195121
Linear SVC's accuracy: 0.6951219512195121
SVM with RBF kernel's accuracy: 0.6859756097560976
MLP classifier's accuracy: 0.676829268292683
Gradient Boosting Machine's accuracy: 0.676829268292683
Random Forest's accuracy: 0.6951219512195121
Decision Tree's accuracy: 0.7042682926829268
---------------------------------
# 使用k-fold
---------------------------------
On dataset: Data/data_combine_0406.xlsx
---------------------------------
Logistic Regression's accuracy: 0.7157601376627263
Linear SVC's accuracy: 0.709037857249738
SVM with RBF kernel's accuracy: 0.7139346102049977
MLP classifier's accuracy: 0.6973664521921292
Gradient Boosting Machine's accuracy: 0.6980547658237318
Random Forest's accuracy: 0.7316549453838097
Decision Tree's accuracy: 0.6845952416579382
---------------------------------

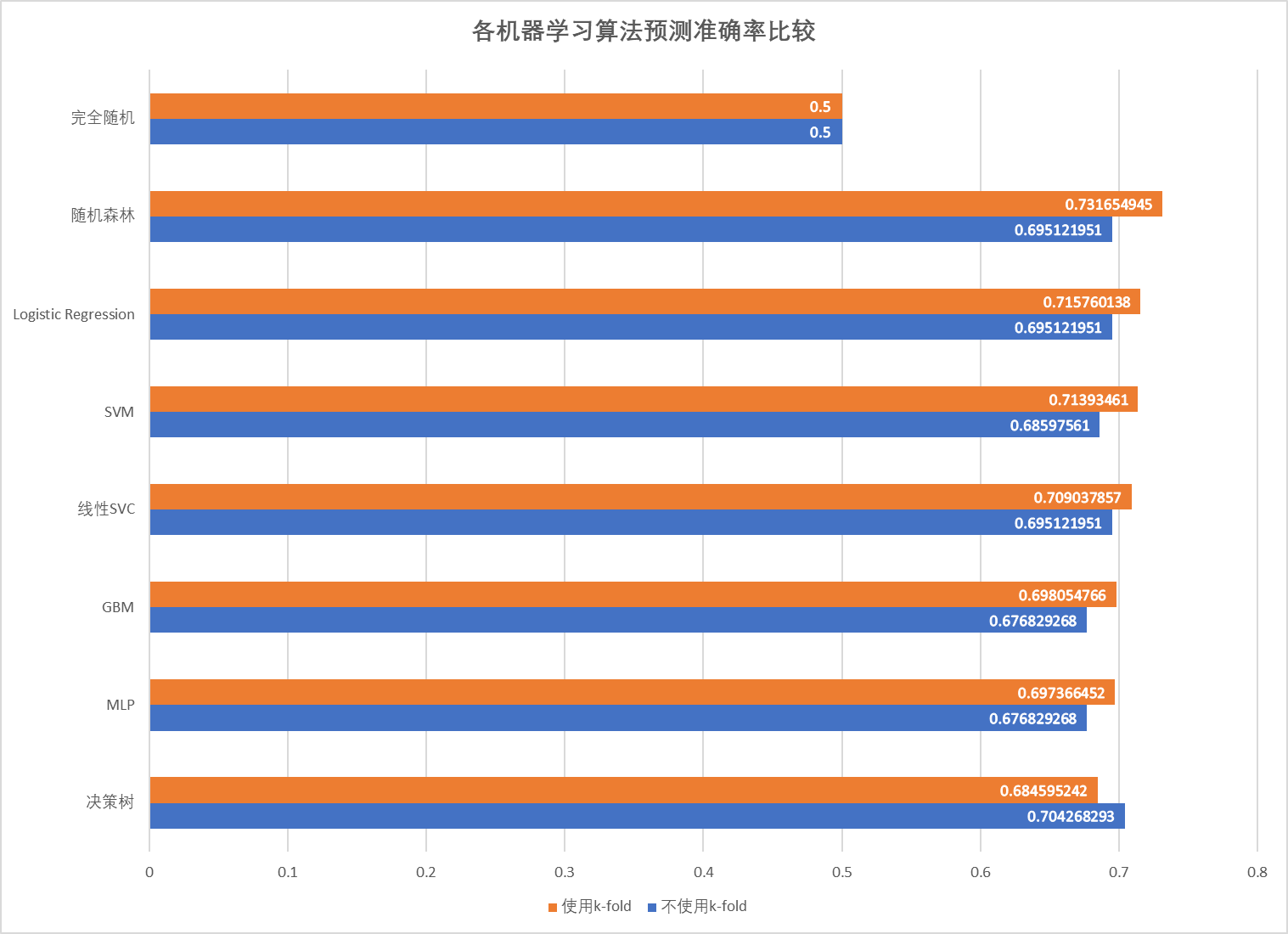
添加一行基础的50%准确率作为对比，各机器学习的方法的Benchmark如下图：

各机器学习算法最终胜率比较

【说起来你数据后面又新增了一批，记得更新结果；也可以试试把数据翻转后再新粘贴上去康康结果】

可以看到预测准确率均在70%左右，而且使用k-fold交叉验证后，除了决策树模型，其他模型的预测准确度都上涨了。

上述算法中，随机森林的预测准确度最高，可能是因为数据中绝大多数特征都是0，而树类算法恰好在稀疏数据上表现良好。

由于MLP我懒得调参【难蚌，后续记得调】，暂时将随机森林的结果作为标准模型。

MLP模型的超参数测试

可以问问jyb这个有什么门道不

【待续】
【后续：1，MLP调超参数分析；2，深度学习；3，基于机器学习或者深度学习的某种算法的包装法分析；4，结论和程序打包】

【hexo似乎对makrdown原生的表格语法不支持】
【一份markdown语法总结】

【关于程序打包，记得学一下别人是怎么配置necessaries那个txt单子的】

【记得整理一下文件夹】

总结

【施工中zzz】